Simple Harmonic Motion
A particle is said to move with S.H.M when the acceleration of the particle about a fixed point is proportional to its displacement but opposite in direction.
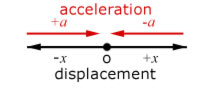
This can be described by the equation:
An equation for velocity is obtained using the expression for acceleration in terms of velocity and rate of change of velocity with respect to displacement(see 'non-uniform acceleration').
separating the variable and integrating,

NB cos-1() is the same as arc cos()
So the displacement against time is a cosine curve. This means that at the end of one completete cycle,
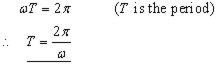
Example
A particle displaying SHM moves in a straight line between extreme positions A & B and passes through a mid-position O.
If the distance AB=10 m and the max. speed of the particle is 15 m-1 find the period of the motion to 1 decimal place.
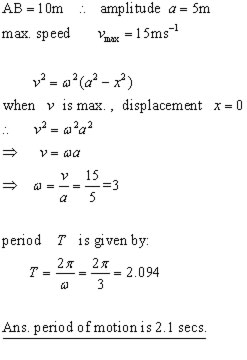

No comments:
Post a Comment